Incredible ChatGPT Math Skills Unveiled: 6 Striking Demonstrations

ChatGPT started off on a bit of a rocky road. People weren’t too impressed with its ability to do the math and make logical sense of things. But let’s give credit where it’s due – the folks over at OpenAI didn’t just sit back. They rolled up their sleeves, made a bunch of improvements, and the result is a whole new and improved ChatGPT. With the latest version – ChatGPT4, they even tossed in a Wolfram plugin, and boy, that’s turned out to be a game-changer.

I wanted to see for myself how much it’s upped its math game, so I threw a mix of math problems at it – everything from your basic add-subtract-multiply-divide, to brain-twisting calculus and stuff even tougher than that.

Once the dust settled, I sat down and took stock of what it could do and where it fell short. And that’s what I want to share with you—a sense of what this improved ChatGPT is capable of and where it might hit a road bump. This way, you can get the most out of using it.

Demonstration: ChatGPT Solving Mathematical Problems

Simple Arithmetic: Addition, Subtraction, Multiplication, Division

We’ve all got to deal with basic math like adding, subtracting, multiplying, and dividing in our daily lives, right? So, let’s see how ChatGPT handles these tasks when we toss ’em its way. Here’s a little chat I had with ChatGPT4 – have a look and see what you think.

My question:

Let’s say you’re planning a party. You estimate that each person will eat 2 slices of pizza, and each pizza has 8 slices. If you’re expecting 15 guests, you’ll need to determine how many pizzas to buy. Then, you want to make sure everyone has 2 bottles of soda, and the soda comes in packs of 6. Additionally, you want to give everyone a goodie bag with 3 pieces of candy, and candy comes in packs of 10. Problem: How many pizzas, packs of soda, and packs of candy do you need to buy?

Let’s see ChatGPT4’s answer:

Let’s break this down item by item:

Pizza:
If each person eats 2 slices, and there are 15 guests, you’ll need 15 guests * 2 slices/guest = 30 slices.
Each pizza has 8 slices, so you’ll need 30 slices / 8 slices/pizza = 3.75 pizzas. Since you can’t buy a fraction of a pizza, you’ll need to round up to the next whole number. Thus, you need 4 pizzas.

Soda:
If each person drinks 2 bottles, and there are 15 guests, you’ll need 15 guests * 2 bottles/guest = 30 bottles.
Soda comes in packs of 6, so you’ll need 30 bottles / 6 bottles/pack = 5 packs. Here, you have a whole number, so no rounding is needed. You’ll need 5 packs of soda.

Candy:
If each person gets 3 pieces, and there are 15 guests, you’ll need 15 guests * 3 pieces/guest = 45 pieces.
Candy comes in packs of 10, so you’ll need 45 pieces / 10 pieces/pack = 4.5 packs. Again, you can’t buy a fraction of a pack, so you’ll round up to the next whole number. You’ll need 5 packs of candy.

So, in total, you need to buy 4 pizzas, 5 packs of soda, and 5 packs of candy.

It nailed it, right? All are neat and tidy with clear explanations. Beats hunting for a calculator most of the time, if you ask me.

Intermediate Operations: Exponents, Roots, Trigonometry

Moving past the basics, let’s talk about exponents, roots, and trig functions.

Exponents are terms that pop up quite often, like when talking about “exponential growth” in the news. Just like multiplication is a faster way to add—like 5 times 3 is the same as adding 5 three times, exponentiation is a faster way to multiply. Say, three times 5 is just multiplying 5 three times—so, 5x5x5.

Exponents come in handy in various areas. In finance, for instance, they help calculate compound interest. You keep reinvesting your profits, and over time, your returns grow exponentially.

Let’s check out how ChatGPT handles an exponential equation. Here are my questions for it:

Solve the following equation:

{6^{2x}} = {6^{1 - 3x}}

ChatGPT’s response:

Given the equation:

6^(2x) = 6^(1 – 3x)

The bases on both sides of the equation are the same (which is 6), so we can set the exponents equal to each other:

2x = 1 – 3x

Next, solve for x:

2x + 3x = 1
5x = 1

Finally, divide both sides by 5 to get:

x = 1/5

So, the solution to the equation is x = 1/5.

As you see, ChatGPT doesn’t just spit out the answer, it takes you step-by-step through the logical process. Here, I used LaTeX to type up the equations, showing ChatGPT can handle this kind of sophisticated mathematical formatting. But you could put the same formula in plain text too, like, 6^(2x) = 6^(1 – 3x).

If exponents are like super-speed multiplication, then roots are the opposite. Say, when you see √ followed by 9, you gotta ask yourself: “Which number times itself equals 9?” The answer’s 3, because 3 times 3 equals 9. This is the essence of roots.

Let’s see if ChatGPT gets the hang of roots in math. Here’s another formula for it:

Simplify

\sqrt{y^2+13}=7

For what value of y is this equation true?

ChatGPT’s response:

Let’s simplify the given equation step by step:

√(y² + 13) = 7

To get rid of the square root, we can square both sides of the equation. Squaring √(y² + 13) will get us y² + 13, and squaring 7 will give us 49.

So, y² + 13 = 49

Subtract 13 from both sides to isolate y²:

y² = 49 – 13
y² = 36

Taking the square root of both sides to solve for y gives:

y = √36

This yields two solutions, as y could be either the positive or negative square root of 36:

y = 6 or y = -6

Therefore, the values of y for which the original equation is true are y = 6 and y = -6.

Typing LaTeX might seem like a pain, but it’s doable to ask the same question in everyday language and get the same result:

Again, ChatGPT serves up the answer and steps in plain language. But can it also provide neat formulas?

The answer is yes, provided you’ve got that Wolfram plugin installed.

The next answer came from ChatGPT with Wolfram onboard:

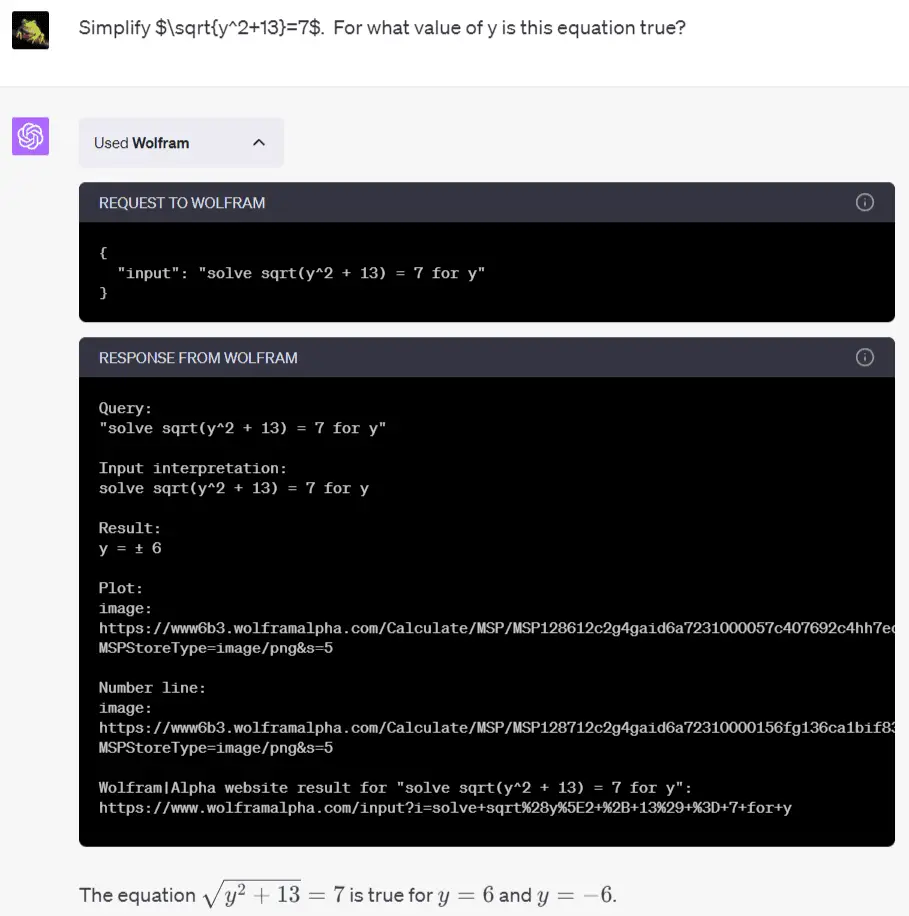
This time, instead of plain language, you get tidy formulas. The answer’s correct, but it doesn’t show you the exact calculation steps.

However, the little black text box above shows the Wolfram calculation process. It pops open when you click the drop-down arrow next to “Used Wolfram”. You can follow the link at the bottom to the WolframAlpha page, like so:

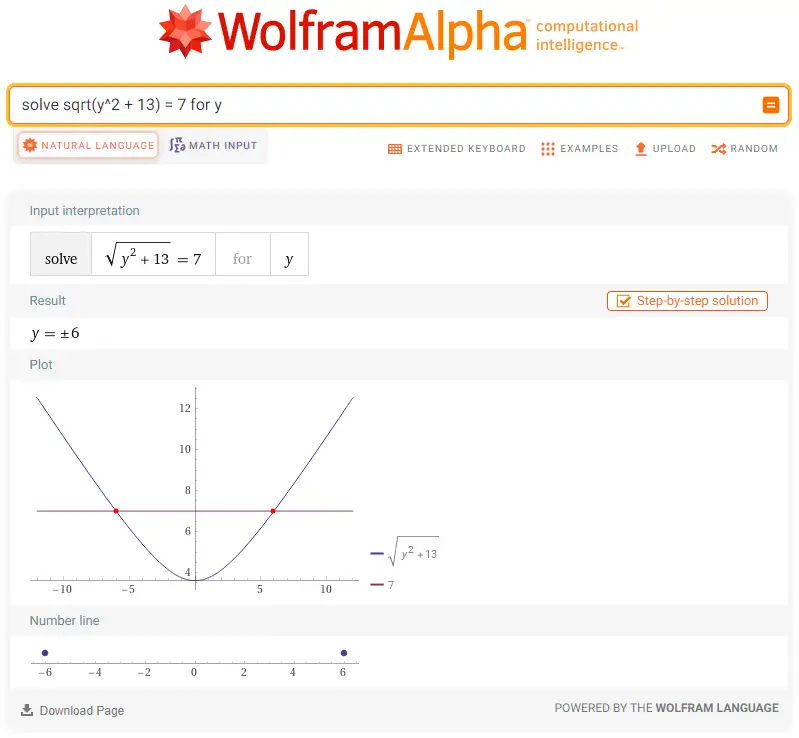
Without me having to lift a finger, I get the answer plus a nice function curve. In essence, after I pitched the problem to ChatGPT, it had a back-and-forth with Wolfram, and then Wolfram translated the problem into a format it could understand to solve it—sqrt(y^2 + 13) = 7 for y.

The Wolfram Language is also a programming language. In the math realm, it can handle not just complex equations but calculus, stats problems, graph theory, and so on. While it’s powerful and quite intuitive with syntax that’s close to everyday language, learning it might be a bit much if you’re not into math, data analysis, or machine learning.

ChatGPT’s arrival has lowered the bar for using the Wolfram language. With the Wolfram plugin, ChatGPT can tap into Wolfram’s powerful language on your behalf, so you can fire away with all sorts of complex math questions.

Next, let’s chat about trigonometry—a tad more complex. It’s like a special toolbox for dealing with triangles and their angles. You know how right triangles have a 90-degree angle, right? Well, trig lets you figure out the length of a side or the size of other angles based on some info you’ve got. It’s super handy in a bunch of professional fields like engineering and architecture.

Check out this trig problem I gave ChatGPT:

\text { Find } \cos \alpha, \tan \alpha, \cot \alpha \text {, if } \sin \alpha=\frac{5}{13} \text { and } \frac{\pi}{2}<\alpha<\pi \text {. }

Here’s ChatGPT’s response:

Given that sin α = 5/13 and that α lies in the second quadrant (π/2 < α < π), we can use the Pythagorean identity to find cos α.

The Pythagorean identity is sin² α + cos² α = 1.

If we solve for cos α, we get:

cos α = ± sqrt(1 – sin² α)

Substituting the value of sin α:

cos α = ± sqrt(1 – (5/13)²)
cos α = ± sqrt(1 – 25/169)
cos α = ± sqrt(144/169)
cos α = ± 12/13

However, because α lies in the second quadrant where cosine is negative, we only take the negative root:

cos α = -12/13

Next, we find tan α using the identity tan α = sin α / cos α:

tan α = (5/13) / (-12/13) = -5/12

Finally, we find cot α using the identity cot α = 1 / tan α:

cot α = 1 / tan α = 1 / (-5/12) = -12/5

So, if sin α = 5/13 and π/2 < α < π, then cos α = -12/13, tan α = -5/12, and cot α = -12/5.

The solution steps are clear, and it seems to be on point. Is the final answer correct? Let’s see what the Wolfram-equipped ChatGPT spits out:

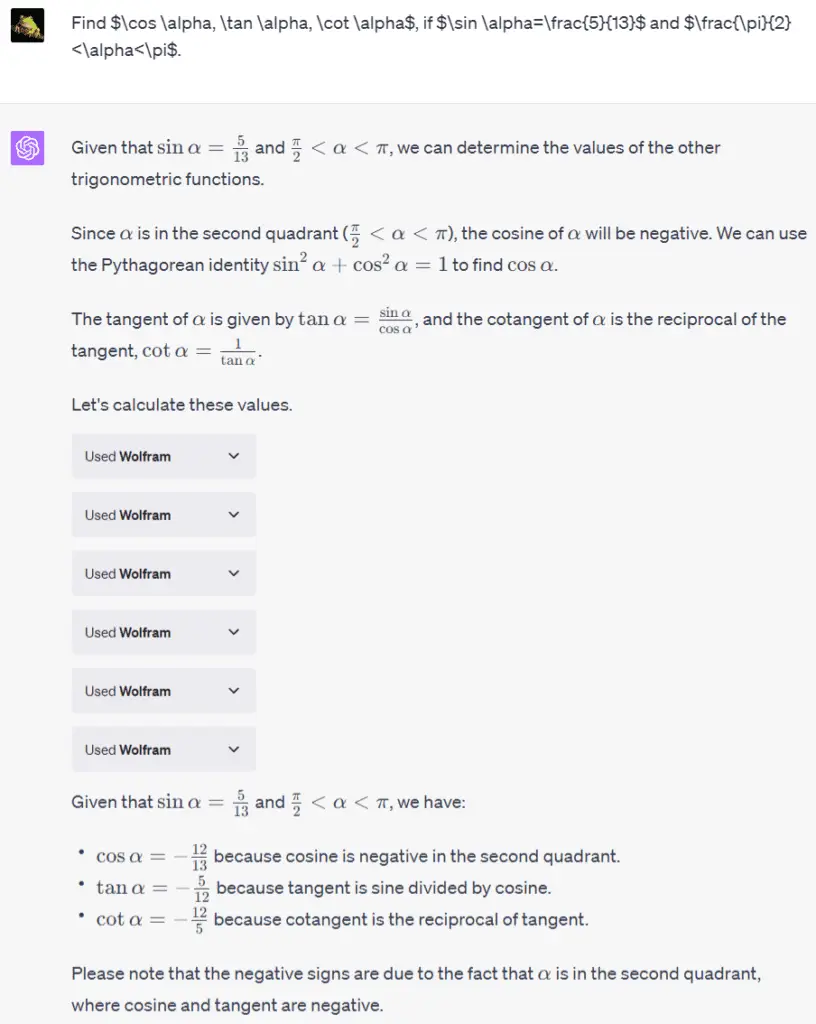
As the figure shows, ChatGPT starts by providing a general solution based on its understanding, then hands over the step-by-step calculations to Wolfram for processing to get the final answer. The outcome matches the one from the ChatGPT without Wolfram.

Advanced Calculations: Calculus and Beyond

Now let’s dive into calculus, the study of change and motion. It has two main bits: differentiation and integration. Differentiation deals with rates of change, like speed being the rate of change of position. It lets us zoom in on instantaneous changes. Integration is about accumulation, like adding up the tiny distances you’ve traveled to figure out the total distance you’ve moved. It’s about adding up a ton of little bits to get an overall picture.

Calculus is used in a wide range of applications. For instance, it helps physicists calculate a rocket’s trajectory, economists maximize profits or minimize costs, and biologists model the growth of species.

Let’s cook up a calculus problem for ChatGPT:

Find the indefinite integral:

\int\frac{1-\ln x}{x^2+\ln^2x}dx.

Here’s what ChatGPT said:

Let’s approach this integral using the method of substitution.

Let’s set: $u = x^5 + x + 1$

Then, the derivative of u with respect to x is: $du/dx = 5x^4 + 1$

Multiplying both sides by dx gives us: $du = (5x^4 + 1)dx$

From the original integral, we can see that the numerator (4x^5 – 1) is a little bit off from our derived du. To fix this, we can rewrite the numerator in the integral as follows:

$4x^5 – 1 = 4(x^5 + x + 1) – 4(x + 1)$

Now, replace $x^5 + x + 1$ with $u$, and $(5x^4 + 1)dx$ with $du$ in the integral: $∫(4u – 4(x + 1)) / u^2 du
= ∫(4/u – 4(x + 1)/u^2) du$

Now, this integral can be broken down into two separate integrals:

$∫(4/u) du – ∫(4(x + 1)/u^2) du$

The first integral can be solved directly as it is now the integral of $4/u$, but the second one still contains $x$, which needs to be dealt with.

Unfortunately, without further information or context, the second integral $∫(4(x + 1)/u^2) du$ can’t be solved with elementary functions, as it involves two different variables ($x$ and $u$). It seems that the integral might have been formulated incorrectly or additional information is required to proceed.

As you can see, even though ChatGPT knows some basic calculus solutions, putting them into action can be a challenge, and the inability to display formulas doesn’t make things clear. This doesn’t mean ChatGPT can’t solve any calculus problem, maybe it can tackle a different one.

Here’s what ChatGPT spit out after I fired up the Wolfram plugin:

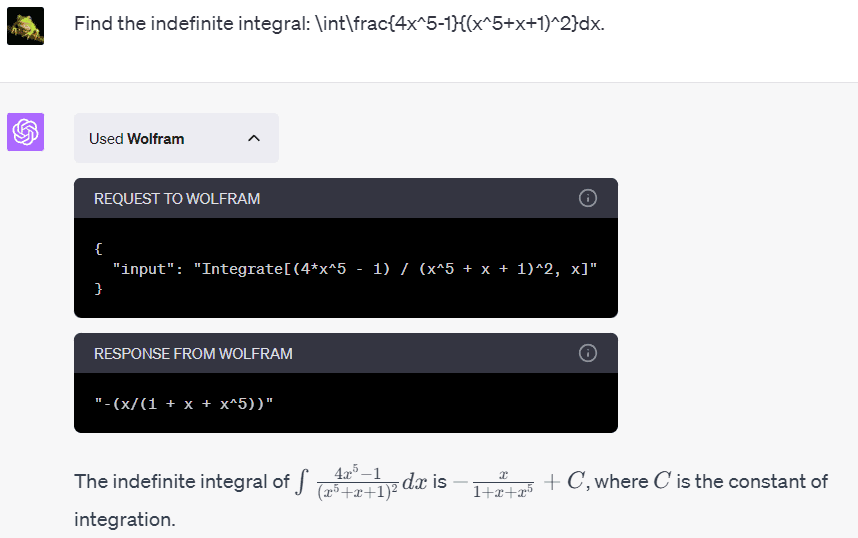
ChatGPT nailed the correct answer in one shot.

You can also head over to WolframApha, punch in the Wolfram language formula “Integrate[(4*x^5 – 1) / (x^5 + x + 1)^2, x]” like in the figure above, and let Wolfram crank out the calculation.

Now let’s look at something a tad more advanced than calculus—differential equations. If calculus is like a game, then differential equations are the boss fights. Calculus is already pretty high-level math, dealing with the accumulation of rates of change and quantities. Moving up a notch to differential equations, you’re dealing with equations based on rates of change in other variables that can model systems where current changes affect future behavior. Like predicting the spread of diseases or modeling climate change, for instance.

Here’s a problem I threw at ChatGPT:

Substitute

y=Be^{3t}

into

y′−y=8e^{3t}

to find a particular solution.

Here’s ChatGPT’s response:

Given the differential equation $y’ – y = 8e^{3t}$ and the solution form $y = Be^{3t}$, we can find the particular solution as follows:

Firstly, calculate the derivative of $y = Be^{3t}$ with respect to t:

$y’ = \frac{d}{dt} \left[Be^{3t}\right] = 3Be^{3t}$

Substitute $y = Be^{3t}$and $y’ = 3Be^{3t}$ into the differential equation:

$3Be^{3t} – Be^{3t} = 8e^{3t}$

Simplify the left side of the equation:

$2Be^{3t} = 8e^{3t}$

Next, divide both sides by $2e^{3t}$:

$B = 8/2 = 4$

Thus, a particular solution to the differential equation $y′ – y = 8e^{3t}$ is $y = 4e^{3t}$.

ChatGPT’s thought process is clear and it serves up the answer.

Let’s check it against the Wolfram plugin’s response:

You see, the two answers match—and they’re both correct!

Let’s take a sneak peek at something special—abstract algebra.

If differential equations are the boss fight in a calculus game, then abstract algebra is like a hidden bonus level. Instead of working with numbers directly, abstract algebra focuses on the structure and patterns behind the numbers. It might seem more abstract (hence the name), but it has some surprisingly practical uses.

In computer science, for example, it helps with things like data structures and debugging code. It’s also used in cryptography—so every time you’re making a secure transaction online, you’re indirectly utilizing abstract algebra!

I found a question from the University of California, Berkeley:

Consider the function

σ : {0, . . . , 15} → {0, . . . , 15}

defined by

x \mapsto\left\{\begin{array}{l}x+4 \text { if } x<12 \\ x-12 \text { if } x \geq 12\end{array}\right.

Show that σ is a permutation and describe its orbits.

Let’s take a look at ChatGPT’s response:

ChatGPT:

A function is a permutation if it is a bijective function, i.e., both injective (or one-to-one) and surjective (or onto).

The function σ is defined from the set {0, …, 15} to itself, and is split into two cases:

1. When x < 12, σ(x) = x + 4. Here, every value of x from 0 to 11 gets mapped to a unique value from 4 to 15, covering 12 distinct values.
2. When x ≥ 12, σ(x) = x – 12. Here, every value of x from 12 to 15 gets mapped to a unique value from 0 to 3, covering 4 distinct values.

Since every element in the domain {0, …, 15} is mapped to a unique element in the same set, and all elements in the set are accounted for, σ is a bijection, and hence a permutation.

The orbits of σ are the sets of elements that map to each other under repeated application of σ.

1. For x in [0, 4, 8], σ repeatedly applied will result in a cycle between these numbers. Thus, one orbit is {0, 4, 8}.
2. For x in [1, 5, 9], repeated application of σ will result in a cycle between these numbers. So, another orbit is {1, 5, 9}.
3. For x in [2, 6, 10], repeated application of σ will result in a cycle between these numbers. Thus, another orbit is {2, 6, 10}.
4. For x in [3, 7, 11], repeated application of σ will result in a cycle between these numbers. Thus, another orbit is {3, 7, 11}.
5. For x in [12, 0], σ repeatedly applied will result in a cycle between these numbers. Thus, another orbit is {12, 0}.
6. For x in [13, 1], σ repeatedly applied will result in a cycle between these numbers. Thus, another orbit is {13, 1}.
7. For x in [14, 2], σ repeatedly applied will result in a cycle between these numbers. Thus, another orbit is {14, 2}.
8. For x in [15, 3], σ repeatedly applied will result in a cycle between these numbers. Thus, another orbit is {15, 3}.

So, the orbits of σ are {0, 4, 8}, {1, 5, 9}, {2, 6, 10}, {3, 7, 11}, {12, 0}, {13, 1}, {14, 2}, and {15, 3}.

Though ChatGPT’s reasoning is well-organized, it doesn’t provide the correct answer. The correct answer is provided below.

Now, let’s see if ChatGPT with the Wolfram plugin can correctly answer this question:

This answer is correct. Wonderful!

So, while ChatGPT may grapple a bit with higher-level math problems, it is still quite capable with the assistance of the Wolfram plugin. You can throw complex equations its way and get accurate, comprehensive answers—even if the problems would make most humans’ heads spin!

What Kind of Math Problems Can ChatGPT Solve

ChatGPT, when paired with Wolfram Alpha, evolves into an impressive problem-solving machine. This symbiotic system couples ChatGPT’s language processing and problem-solving finesse with Wolfram Alpha’s computational wizardry and mathematical prowess.

Here’s a quick tour of the mathematical territories this powerhouse system can conquer:

• Arithmetic Operations and Algebraic Equations: It comfortably handles basic arithmetic problems and tangles with complex algebraic equations. Wolfram Alpha offers precise solutions, while ChatGPT, where possible, serves up easy-to-follow step-by-step guidance.
• Calculus: Be it derivatives, integrals, limits, or differential equations, this combined system doesn’t flinch. Wolfram Alpha delivers rapid, accurate calculations, and ChatGPT can often break down the process and underlying principles into palatable chunks.
• Linear Algebra: With ease, it solves problems involving matrix operations, determinants, and the mysterious eigenvectors and eigenvalues. Wolfram Alpha does the number crunching, and ChatGPT makes sense of it all in a relatable manner.
• Trigonometry: Simplifying trigonometry, solving equations, and explaining the workings of various trigonometric principles is part of its repertoire.
• Discrete Mathematics: Step into the world of number theory, combinatorics, and graph theory with this system. Expect prime factorization, modular arithmetic, and permutations and combinations, as well as mysteries of graph theory to be unraveled.
• Probability Theory and Statistics: Probability distributions, hypothesis testing, regression analysis, and Bayesian inference problems meet their match here. Wolfram Alpha provides precise calculations, while ChatGPT often demystifies complex statistical concepts.
• Geometry: Points, lines, shapes, and solids are all part of its playground. Expect to find solutions for areas, volumes, and even geometric proofs.
• Differential Equations: Ordinary or partial, no differential equation is too big a challenge for this team.
• Logic and Set Theory: Propositional logic, predicate logic, and set operations are well within its grasp.

So, whether you’re an arithmophobic looking to conquer basic operations or a mathematics enthusiast ready to wrestle with complex problems, this union of ChatGPT and Wolfram Alpha stands ready to assist.

The Limitations of ChatGPT in Math

No doubt, the marriage of ChatGPT and Wolfram creates a powerful tool for math problem-solving. However, like every other tool, it isn’t perfect. Math is a precision science, and understanding the capabilities and shortcomings of this duo can help you make the most of them while avoiding potential pitfalls.

Here are a few bumps you might hit on the road:

• Contextual Understanding: Despite its collaboration with Wolfram Alpha, ChatGPT sometimes fails to accurately grasp the context. You might need to nudge it with precise cue words to get the desired response.
• Slightly Off-Key Duo: Wolfram Alpha delivers step-by-step solutions and ChatGPT churns out detailed explanations. But, they don’t always sing in perfect harmony. There might be cases where the quality or accuracy of one doesn’t quite match the other.
• Struggling with Complex Problems: Wrestling with highly intricate problems is a bit of a challenge for ChatGPT. Wolfram Alpha, on the other hand, sometimes stumbles over abstract math. As a result, this pair might not be the best fit for advanced theoretical problems, multi-step problems, or providing rigorous proofs.
• Limited Computational Muscle: For exceptionally complex calculations or massive equation systems, the duo might find it hard to deliver if the computation becomes too hefty.
• Access Limitations: It can only provide rough answers at times. To get a more polished solution, you might need to pay a visit to the Wolfram Alpha website. Plus, accessing some of the advanced features there needs a Pro version subscription.
• Limited Expertise: While ChatGPT leans on Wolfram Alpha for detailed calculations, the results they spit out for complex equations or critical applications should be double-checked by human experts.
• Blind Spot for Visual Data: Due to the visual data processing limitations of both tools, they might not be able to make sense of graphical information in math problems.
• Internet Dependency: ChatGPT and Wolfram Alpha are online tools. Without a stable internet connection, they’re as good as non-existent.

Remember, while this ChatGPT-Wolfram duo is mighty useful, it’s no substitute for human ingenuity and precision in mathematics.

Summary

This blend of ChatGPT and Wolfram’s computational prowess is a potent tool for anyone studying or working in fields that require heavy-duty mathematics. It not only makes understanding and solving complex problems easier but also makes learning mathematics more fun and engaging.

As AI technology continues to evolve, I believe we’ll see even more capabilities like these that significantly enhance learning experiences and professional work across numerous domains. Math is just one area where AI like ChatGPT can have a substantial impact—imagine the possibilities in fields like physics, chemistry, economics, and more!

So, don’t be shy about exploring and experimenting with ChatGPT and the Wolfram plugin, whether you’re brushing up on basic math or diving into more advanced territory. The AI is ready and waiting to tackle your toughest questions!